Úvod

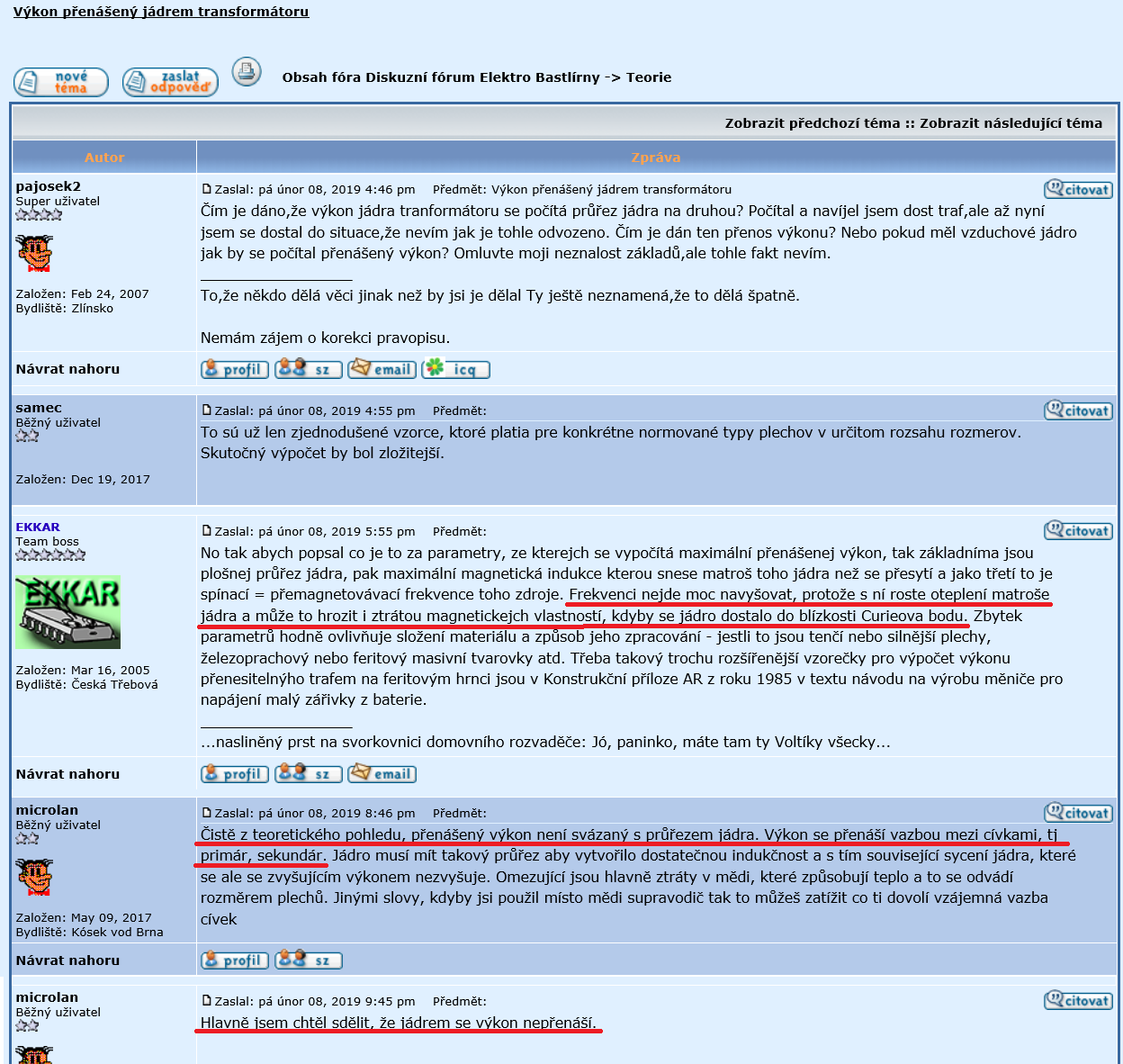
Člověku by se zdálo, že stokráte nic unaví i vola, ale nikoliv Team bosse EKKARa na Bastlírně si vždy najde jak člověka rozesmát či pobavit a jak jinak než způsobem člověka trpícího nejenom elektrotechnickým kretenizmem, tedy způsobem jemu vlastním, nyní se zaměřil při výpočtu transformátoru na Curieovu teplotu (Tc).

Team boss EKKAR na Bastlírně sice elektronice či elektrotechnice moc či vůbec nerozumí, jak stále dokola dokazuje, ale píše příspěvek za příspěvkem a to co největší šířky a nejméně k věci, jen aby oslnil svým záběrem a udržel pozornost svých oddaných příznivců, přitom se jedná o učivo 15letých dětí, tedy učiva dětí v prvním ročníku učilišť a středních škol, ale s Curieovou teplotou to moc nesouvisí, neboť za běžnou teplotu je brána teplota 20°C, a výrobky se staví až po pracovní teploty 60, 80, 85 či 105°C, teploty vyšší se běžně nepoužívají.

Curieova teplota pro feromagnetické železo, které je nejčastější materiál u síťových transformátorů použit k výrobě jádra, a k čemuž směřoval původní dotaz, je Curieova teplota uctihodných 1043°C a pro lepší materiály jako je feromagneticky Cobalt, je tato teplota až 1388°C, při této teplotě bychom již měli dávno roztaveno i měděné vinutí, což Team bossu EKKARovi na Bastlírně zjevně nedochází, stejně jak fakt, že při těchto teplotách většina používaných materiálů již dávno hoří.

Prostě se počítá od I a N přes Um, H, B a Ø, vše se musí podřídit přijatelnému B, pro které je důležitý nejenom průřez jádra S, ale také počet závitů N, přičemž většina transformátorů se navrhuje pro pracovní teploty do 85°C či teplotu podobnou, k čemuž se často jistí tepelnou pojistkou.

Někteří se mylně domnívají, že se jádrem výkon nepřenáší, opět se vrátím k učivu prvních ročníků, je třeba si uvědomit, že na vstupu je proudové pole se svým vstupním proudem, energie se musí přenést do pole magnetického, kde získáme magnetický tok Ø, který je celý soustředěn v železném jádře, a následně se musíme vrátit zpět indukovaným napětím Ui do pole proudového, tento fakt je o to více zřetelný u autotransformátorů, kde se část energie přenáší přímo za pomocí elektrického proudu polem proudovým a část je transformována přes pole magnetické či elektromagnetické, ve výsledku si vystačíme s menším transformátorem, ale za cenu galvanického spojení primárního a sekundárního vinutí. 

Tato série článků věnována Team bossu EKKARu na Bastlírně je mementem toho co se dnes a dlouhá léta na internetu vyskytuje a odehrává, kde je publikováno stále více nesmyslů jak smyslů a mnozí plodí kravinu za kravinou a jsou jich desetitisíce jen aby ozářili svým nadhledem a rozhledem co nejvíce svých obdivovatelů, ale realita je často někde zcela jinde, jen se často melou kraviny s problematikou nesouvisející, jak je názorně vidět výše,  tak se pomalu ale jistě stávají nejenom takové příspěvky, ale často i weby pro mnohé až životu nebezpečné a lidé organizovaně hloupnou a hloupnou, namísto toho aby se se znalostmi posouvali dále.

Snad spíše jako Aprílovou vložku s velkým A jsem přidal směr vývoje diskuze, kde do magnetizačních vlastnosti vstupují i hodnoty jiné než bychom mohli kdy čekat. Vždy jsem vycházel z toho, že u rovnice se musí levá strana rovnat straně pravé, a to nejenom co se hodnot týče, ale hlavně co se rozměrů týče, jinak je vše špatně a uvedený příklad je více než špatně.

Zde předvedené a uvedené je naprosto unikátní, není se čemu divit, neboť v minulosti se ne ElektroBastlírně obdobným způsobem počítaly příklady z přijímaček na střední školu, které prověřují znalosti ze základní školy, na deset odpovědí připadalo alespoň patnáct totálních nesmyslů, stejně jako zde  při počítání výkonu přenášeného jádrem transformátoru.

Pokračování den třetí

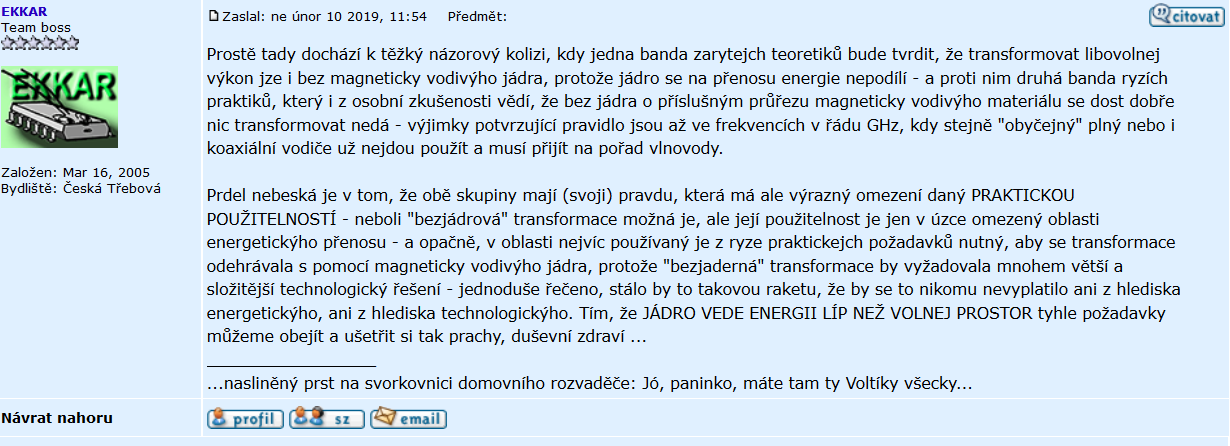
Třetí den vášnivé diskuse, kde se krom proudového a elektromagnetického pole se neopomene ani Curieova teplota, rychlost světla i gigahertzové frekvence, vyšší matematika a integrály jalové složky, přitom nepochopení síťového transformátoru, zato se soustavnými odbočkami a kličkami v zájmu vlastní důležitosti působí opravdu úsměvně, tím nechci říci, že se jedná o úroveň jen ElektroBastlírny, je to dnes obraz účastněných diskutujících, často anonymních.

Není to problém jen ElektroBastlírny, je to problém dnešní společnosti, kdy je vše na internetu, ale již nikoho moc nezajímá zda je to blbost či nikoliv, tak se autority postupně zlikvidovaly a prosadili ti kteří jsou vytrvalí a líp se houfují, aby své kořisti uštvali a napsali více příspěvků jak konkurence, obrazem společnosti se tak stává neúcta ke všemu tradičnímu, v neposlední míře k sobě sama.

Diskuze se vyvíjí směrem rozdělení na neznalé a ještě neznalejší, což není to pravé na cestě k poznání. Jak jsem již napsal dříve, je třeba začít u pole proudového u proudu I [A] a počnu závitů N [-] a dostat se k poli elektromagnetickému Um=I*N [A=A*-].

Abychom se vrátili zpět, k poli proudovému k indukovanému napětí  Ui, musíme vyřešit ΔØ/Δt kterému je rovno. Magnetický tok vypočteme jako Ø=B*S [Wb=T*m²], kde B je magnetická indukce rovna B=µo* µr [T=H/m-1*-], µo je konstanta na nás nezávislá, µr je materiálová konstanta, které jsme se naučili dělit dle označení materiálů na Dia, Para a Fero, jak je patrné s názvu Fero, jde o materiály postavené na bázi železa, ty mají µr>>1, je tedy účelné použít právě takové materiály. Pro síťové transformátory se používají materiály převážně s 2000˂µr˂5000, čímž dosáhneme značné magnetické indukce.

Jenže na cestě k maximálnímu magnetickému toku nám stojí ještě plochá S, kterou obepíná cívka, v níž se má napětí indukovat, abychom nemuseli neúměrně plochu zvyšovat, je více než účelné svést do jejího středu většinu magnetického toku feromagnetikem, které má µr krát větší magnetickou vodivost než vzduch. Nesmíme zapomenout na fakt, že na tvorbě napětí Ui se podílí jen magnetický tok procházející cívkou, musíme tam tedy svést všechen magnetický tok vytvořený vstupním proudem, tedy primárním vinutím, jinak by se nám tento poměr přímo podílel na poměru transformačním větší měrou než účinností ξ. Nyní se dostáváme k indukovanému napětí, na jehož vstupu máme opět veličiny proudového pole Ui= Δ((S*µo*µr*I*N)/l)/Δt.

Jak je patrné na vstupu máme proud, nikoliv napětí, abychom se dostali k napětí, museli bychom vypočítat U=I*Xl, při Xl=ωL, musíme vypočítat samotnou indukčnost L, třeba jako L= Ø/I [H=Wb/A] či L=N²*µo* µr*S/l, zde je patrné, že užití materiálu s velkým µr nám ušetří na počtu závitů, ale také na velikosti samotné konstrukce.

Rozuzlení

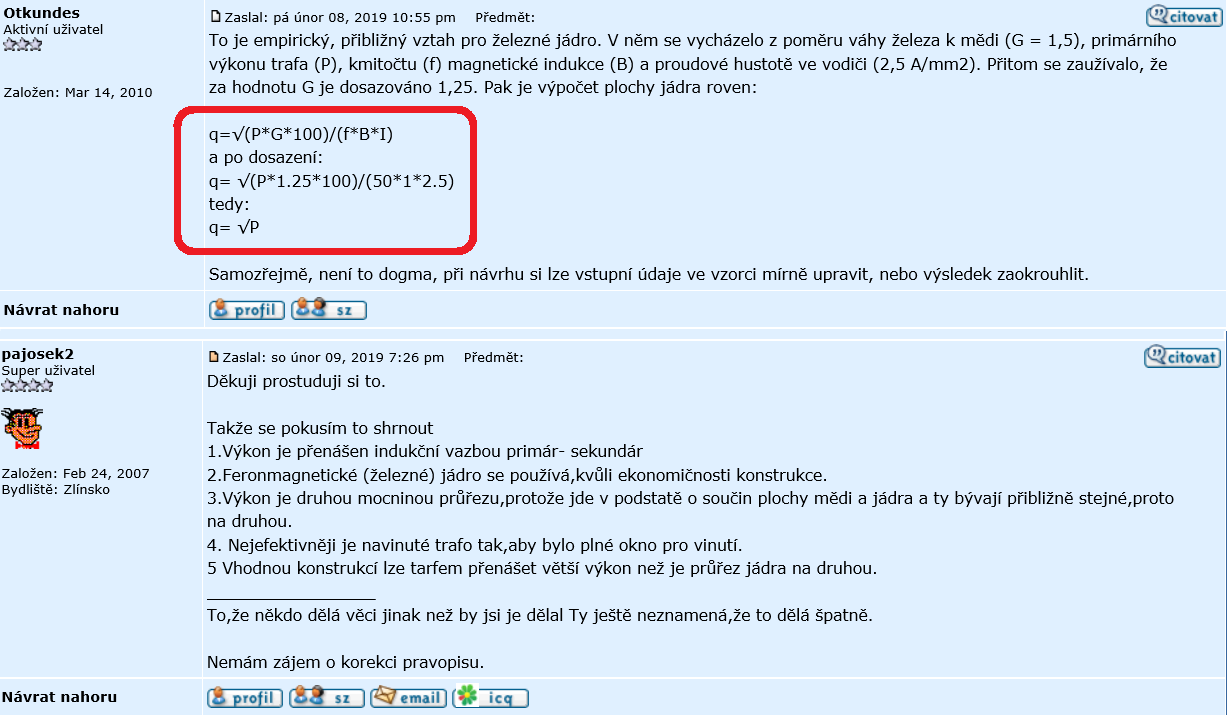
Abych se vrátil k původnímu dotazu, a sám zodpověděl proč je výkon právě plocha jádra v (cm²)², no právě proto, že se vycházelo s frekvence 50Hz, µr pro běžné EI transformátorové plechy, sycení jádra B=1T, dost či hodně praxe, pracovní teplota do 80°C, plocha primárního vinuti pro 230V cca 40% plochy pro vinutí, což zamícháno do jednoho výpočtu a je to matematicky téměř neodvoditelné, neboť musíme do výpočtu ještě přidat izolace a prokládání vinutí. Sycení jádra je dáno spíše proudem jalovým, tedy v nezatíženém stavu, výstupní proud je pak transformován do primárního vinutí se stejnou fází, vzniklé sycení těmito proudy jsou protisměrné, tudíž se na výsledném sycení jádra moc nepodílí.

Pro jiné plechy, například C či toroidy se používají jiné materiály a taky jiné, větší sycení B. Dále jsou zaužívány i další zjednodušení výpočtu EI transformátorů, jako počet závitů na Volt jako N=45/Sfe, kde konstanta 45 vychází dost přesně ze sycení jádra 1T, jako další zjednodušení se často užívá průměr vodiče Ø=√(I/2), což dost přesně platí pro proudovou hustotu J=2,5A/mm².

Takto nějak či jednodušeji měla vypadat odpověď na původní dotaz, ale zjevně komunita na ElektroBastlírně mluví diametrálně jiným jazykem, zabíhajícím často do všech možných stran a problematik, aniž by jim většinou jakkoliv rozuměli, prostě cizím jazykem ke kloudnému výsledku nevedoucím, jinak buďme rádi, že nám naši předci takto výpočty zjednodušili.

Vycházet z poměru váhy mědi a železa je poněkud zavádějící a není možný, neboť zaplněnost jádra počítáno s izolací a tedy i množství mědi, není v žádném případě konstantní, pro EI10x10 by vyšla potřeba plochy jenom pro primární vinutí daleko přes 400% mezery, pro EI16x16 je to stále přes 100%, pro EI 20x20 je to ještě 78%, což silně omezuje možnosti cokoliv namotat, ale již se nám vejde alespoň primární vinutí, pro EI25x20 se již dostáváme na potřebu 62%, a až při EI32x32 se blížíme k 50% přesněji je to 52% a tak dále pro EI 70x70 jsme již na 38%, a pro EI100x100 již jenom 35%, a máme tak dostatek prostoru pro sekundární vinutí. Počítáno pro kostřičku s 1,5mm materiálu, primární vinutí prokládáno kondenzátorovým papírem 2x0,05mm a zakončeno papírovou izolací 2x0,5mm.

Vzoreček q=√(P*G*100)/(f*B*I) je naprosto fantastický, bez vinutí, při nepoužití mědi dostaneme nekonečný přenášený výkon, naopak čím dáme mědi více, tím menší výkon přeneseme.

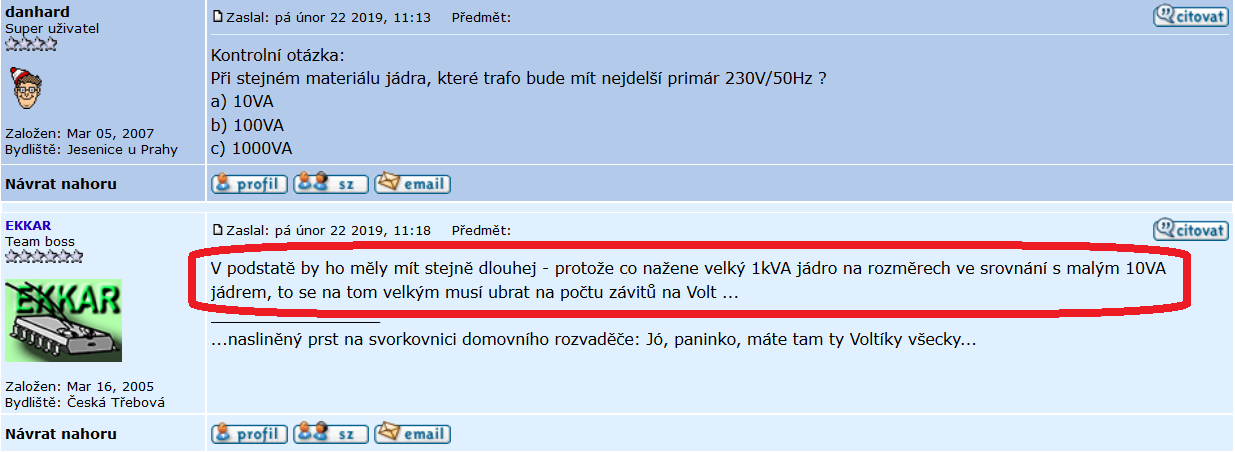
Plocha tedy i výkon roste s kvadrátem, spolu s poklesem počtu závitů, kdežto rozměr tedy obvod roste lineárně stejně jak délka jednoho závitu, ach ta malá násobilka.